|
I've been to about a million PD sessions on Spiralling the Curriculum in Math classes over the last few years but I haven't heard much about spiralling in Science classes. This semester I had an opportunity to teach Grade 11 Physics (SPH3U) for the first time in a while and really wanted to give it a shot. This is what I came up with.
If you aren't familliar with Spiralling, this post by Mary Bourassa is what got me started with my 10 Applied Math classes a few years ago. It's basically rearranging the course in Cycles instead of Units. Each Cycle contains bits from each of the curriculum strands. The complexity of the course material increases throughout the course. It's been a big success so far. Half way through the semester my students have already seen about 70% of the material in each of the strands from the course. There will be no need to cram in the Electricity unit or Sound unit at the end of the course since they've already seen a bunch of each of those strands. Also, Spiralling is much less restrictive in that I can change the topic whenever the students need a change and provides tons of opportunities to make connections between the different strands. My hope is that students will remember much more of the material at exam time and exam review will be relatively easy. I've also used a combination of Peter Liljedahl's Thinking Classroom and the Flipped Classroom which has freed up class time for discussing and tackling difficult problems. If you're interested in the what research says about the advantages of Spiralling, it mostly has to do with how students learn and Cognitive Load Theory. I recommend Make it Stick and How I Wish I'd Taught Maths. Drop me a line if you want to discuss this more!
2 Comments
Craig Barton takes a look at how student brains learn and think and uses that to inform his teaching. This book has changed the way I see teaching math. Here is my 1 page summary:
So often is this question asked by lost students in Math and Science classes. With a background in Engineering, I am always looking for ways to integrate STEAM projects into my Math and Science classes to help students make real-world connections.
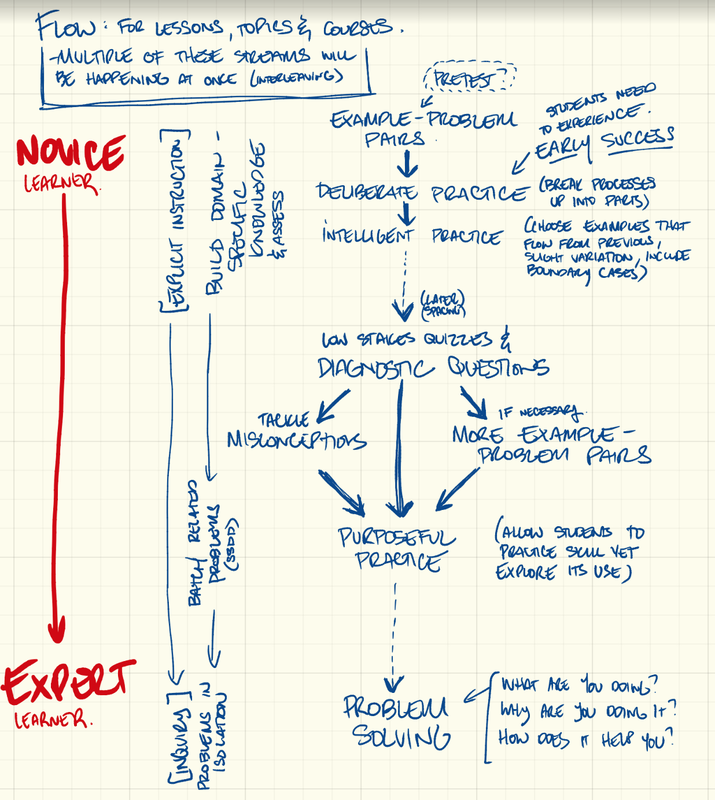
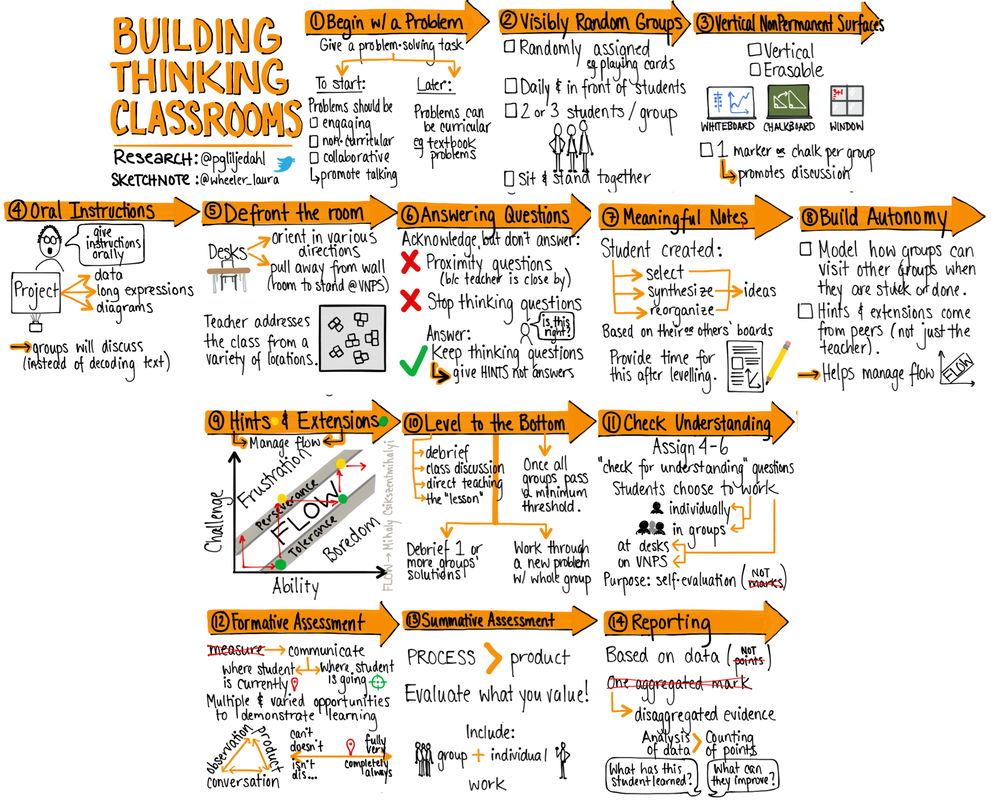
Inspiration struck after seeing Peter Liljedahl present at OAME 2018. He provides a framework of how to Build Thinking Classrooms based on his research. (Image below from https://mslwheeler.wordpress.com/2017/11/18/3497/) I have been working on incorporating mostly 1-4 in my classes so far but are working towards the rest. Especially interesting is how the framework incorporates 21st Century competencies, especially...
Play with the projection of a vector on another vector...
My Calculus students needed some work with piecewise functions, and seemed to enjoy the slope puzzles we had been doing periodically so I had them create their own as a mini assignment.
The requirements were:
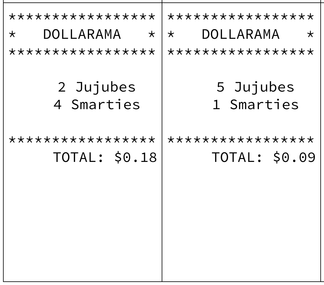
Here is an example of one of the really interesting submissions: The rest of the submissions: Samantha and Katherine (Reciprocal): https://www.desmos.com/calculator/k6ta1hpjr1 Melvin (Polynomial): https://www.desmos.com/calculator/pcytghpgp2 Malcom and Jonathan (Absolute value): https://www.desmos.com/calculator/s18vpu6eyt Ahillan (Sine): https://www.desmos.com/calculator/moj40jbkeg Gerardo and Patrick (Sine): https://www.desmos.com/calculator/02bxuszbjn Jose (Cosine): https://www.desmos.com/calculator/i9jqcvknsw Nana S (Sine): https://www.desmos.com/calculator/7aam6jjs0p Lucas (Polynomial): https://www.desmos.com/calculator/84qr54wycg Almendra (Sine): https://www.desmos.com/calculator/gkoosz85js Noyangbe (Radical): https://www.desmos.com/calculator/ycku94ltoe Monica (Radical): https://www.desmos.com/calculator/xm17lhvipf Lawrenda (Polynomial): https://www.desmos.com/calculator/x4wxfuoerk Nardos and Priscilla (Cosine): https://www.desmos.com/calculator/70rrejqt3y Mirabel (Polynomial): https://www.desmos.com/calculator/ttg4pb1uf9 Brian and Joshua (Reciprocal): https://www.desmos.com/calculator/c0ucoms3w5 Jad and Nathan (Sine): https://www.desmos.com/calculator/h6u1bbz00f Faith (Sine): https://www.desmos.com/calculator/t9ujrlfflz Donovan and Ranvir (Reciprocal): https://www.desmos.com/calculator/hz19ixgc0k Anitha (Sine): https://www.desmos.com/calculator/0kxlczcguw Jayestha (20th degree polynomial, sine, absolute value): https://www.desmos.com/calculator/xghnljuqcu Ethan (Reciprocal): https://www.desmos.com/calculator/llggi5zedd Nana O and Michael (Root): https://www.desmos.com/calculator/dlfqhn8cuu Kurtis (Reciprocal): https://www.desmos.com/calculator/bnrqwevbne Course: Grade 10 Applied Math, Topic: Finding surface area After seeing Andrew Stadel's File Cabinet 3-Act Lesson, we thought it would be an easy one to do with our 10 applied classes near the beginning of the semester. We didn't just want to watch the Andrew Stadel video though, we wanted our students to actually cover an iPad cart with post-its. After going through the Andrew Stadel 3-Act lesson as a class, I put a few post-its on the cart. After recording some initial estimates, they immediately got to work measuring and calculating... "But it would take a whole period to cover the whole cart with post-its! How on earth do you have time for that???" Not every student needed to be involved. After a quick lesson on calculating surface area, I asked the 2 or 3 students who finished the surface area practice problems quickly or the students who were finding it too easy to do it. As the rest of the class practiced calculating surface area, they stuck 'em on. It did end up taking the better part of a period but those students were happy to do it! The anticipation in the class grew as more an more post-its were added. It was super satisfying for everyone to get a final, definite answer (see video below). It was also great to see the Grade 9's and 12's who came into the classroom afterwards spontaneously start asking questions about the post-it covered cart. "Can we do more lessons like that too?" Course: Grade 10 Applied Math, Topic: Using Elimination to solve systems of equations. I brace myself for the classic question from students, "But when are we ever going to use this???" But the question never comes, since they already know the answer: to find the cost of Jujubes and Smarties from a receipt, obviously. Shamelessly appropriated from Alex Overwijk at Slam Dunk Math by my teaching partner and I, this activity is one of our favourites from the semester. The kids love it too. They get to problem solve and eat some candy while doing it. Setting the stage: I show the students a receipt from Dollarama. What am I gunna ask you to do? Aside from the obvious, "Who buys 4 Smarties?" they come to "How much does one Smartie and one Jujube cost?" fairly quickly. So can we figure it out? After coming up with a few different possibilities for the costs by manipulating the Smarties, Jujubes and "pennies", the conclusion is nope. There is more than one possible answer. What about if I had another receipt from the same store? Now we're getting somewhere. The cost of a Smartie and Jujube has to work for BOTH receipts! The Activity: After working through the example together, receipts from various stores are distributed randomly to each student in the class. They then have to find their partner (the person who has a receipt from the same store as them) and come up to the front to get actual Smarties, Jujubes and "Pennies" (plastic squares) and then figure out how much a Smartie and Jujube costs at that store by trying different combinations with the manipulatives. When they have an answer, they check with the teacher and are given 2 new receipts from a different store. After they solve their required 4 pairs of receipts, they ask for more. That's when I throw one at them that doesn't have a integer solution, or one that has multiple solutions and let them debate it out amongst themselves. After the activity: You folks realize you solved some pretty complicated math problems today? Awesome work. What about if I gave you a problem like this? They realize it's not practical to use physical Smarties and Jujubes to solve the problem. If only there was an easier way...
Cue Elimination, with a distinct lack of "Why are we learning this."
Get an intuitive understanding of how the slope of a tangent can be approximated with a secant...
Play with the Desmos file by opening it in the Desmos web app.
Why is Calculus only taught in Grade 12? Students need to have the algebra background to be able to calculate "difference quotients" and manipulate limits.
But do you need to be proficient in algebra to understand Calculus? Nope. You just need a basic understanding of rate of change. "Slope Puzzles" have students predict the graph of the derivative of a piecewise function. The answer is revealed by sliding the black point to the right...
Link to Slope Puzzle 1 Desmos
I believe there is way too much emphasis on algebra in the high school math curriculum. Not enough time is spent building a deep understanding of the concepts.
Even though it's saved for the end of Grade 12, as a rite of passage to mathematical prowess, differential calculus isn't a difficult concept! Even my Grade 9's could solve this puzzle after some practice.
Link to Slope Puzzle 2 Desmos
Solving these puzzles builds an intuitive understanding of differentiation without having to perform any algebra at all. I plan on using these puzzles in my Calculus class from the first day of the semester to help build that intuition.
I also plan on having Calculus students create their own Slope Puzzles in Desmos as a way to test their understanding of piecewise functions and function continuity. |
Lukas NottenTCDSB Educator Archives
November 2019
Categories |
















 RSS Feed
RSS Feed